גילוי קצוות
פיקסל בתמונה נחשב ל"קצה" אם הפרש העוצמות בינו לבין שכנו (מימין או משמאל, מלמעלה או מלמטה) הוא גדול. כמה גדול? בד"כ אני נוהג למצוא את הסטטיסטיקה של הבדלי העוצמות הללו ולבטא את ההפרש ככפולה של סטיית התקן של התפלגות הפרשי העצמה.
אם במקום התמונה המקורית נבנה תמונה חדשה שבה פיקסלים שהם "קצה" בתמונה המקורית ייצבעו בשחור, וכל אותם פיקסלים שאינם "קצה" ייצבעו בלבן, נקבל תמונה המזכירה רישום:

בהירות התמונה ועובי הקווים תלויים בסף שבו בחרנו להגדרת "קצה". בטבלה למטה "קצה" הוא כל מה שחורג מ-0.5, 1, 1.5, ו- 2 פעמים סטיית התקן של התפלגות ההפרשים בתמונה:



סף: 0.5 סטיית תקן

Describe your image.



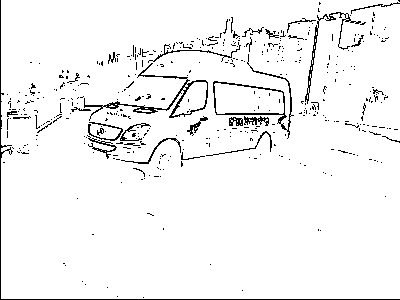
כמה צריך להיות הסף? את זה אני בוחר בכל תמונה מחדש.
מתי טכניקה זאת טובה ומתי לא? מה היתרונות והחסרונות?
נופים אורבניים: בתים, עצים בודדים, עמודי חשמל, תבניות על המדרכה, סורגים וכדומה נראים בד"כ טוב מאד. עצמים שבהם הקונטרסט משתנה בהדרגה, כדוגמת פרצופים, מכוניות וכו', נראים פחות טוב. הדבר הבעייתי ביותר בטכניקה זאת הוא צל. גבולות הצל נראים בד"כ בבירור, אך הצל עצמו נראה לבן ולא שחור, בגלל היעדר קונטרסט בתוך הצל עצמו. גם נופים טבעיים (הרים, שיחים, וכו') - אינם נראים טוב, בגלל ריבוי הפרטים. לעומת זאת קו המיתאר בין ההרים לשמיים נראה מצוין, אם זה הדבר שרוצים להראות.
הנה כמה דוגמאות:

נוף אורבני טיפוסי (רח' חטיבת עציוני בכרמיאל). הבתים, מתאר העצים, תמרור הרחוב והסימונים על המדרכה נראים היטב בתמונה.

נוף עירוני בסינגפור, על יד תחנת הרכבת התחתית little india. גם כאן הבתים, מעקה הברזל, פסל הטווס והעצים נראים היטב.

צמחייה בסינגפור. יש לשים לב כיצד האזור המוצל שבין הצמחים מופיע בהיר במקום כהה.


שיכונים, בתי דירות וגורדי שחקים בסינגפור. מבט מרחוב orchard צפונה
מספר דוגמאות שליליות:

פרצופים לא נראים טוב. הקונטור החיצוני מוגזם, ואילו הפרטים בתוך הפנים מיטשטשים. שיער חלק, גם אם הוא כהה, נראה בהיר, וכן הלאה.

נופים טבעיים (הרים, שיחים, וכו', במקרה זה הה�ר שעליו צורית וגילון, עם הכביש לכניסה המערבית לכרמיאל) לא נראים טוב. ריבוי הפרטים נוטה לטשטש את הפרטים החשובים והמעניינים שבהם צייר היה מתמקד, תוך טשטוש האזורים הפחות מעניינים.
